 Home
Home
 Back
Back
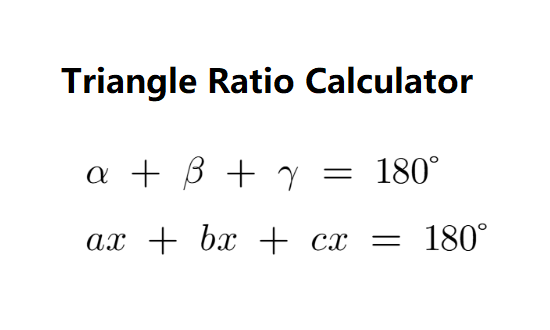
Triangle Angle Ratio Calculator calculates the angles of a triangle based on the given ratio of angles (a:b:c).
It is useful in geometry and trigonometry to determine angle measures and corresponding side length ratios when their proportions are known.
To calculate the angles, input the angle ratios (a:b:c). The formula used is based on the fact that the sum of angles in a triangle is 180°:
α + β + γ = 180°
If angles are in ratio a:b:c, they are expressed as ax, bx, and cx, where \( x = 180 / (a + b + c) \).
Side length ratios are derived using the Law of Sines: \( \frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)} \), normalized with the first side set to 1.
Use the form above to input the ratios, and the calculator will provide the angles and side length ratios.
Example: Suppose the angle ratios are a = 1, b = 2, c = 3.
Calculate x: \( x = \frac{180}{1 + 2 + 3} = \frac{180}{6} = 30 \)
Angles: \( \alpha = 1 \cdot 30 = 30^\circ \), \( \beta = 2 \cdot 30 = 60^\circ \), \( \gamma = 3 \cdot 30 = 90^\circ \)
Side ratios (using Law of Sines, normalized with first side as 1): \( \sin(30^\circ) : \sin(60^\circ) : \sin(90^\circ) \approx 1 : 1.732 : 2 \), normalized to 1 : 1.732 : 2.
Enter these values (a = 1, b = 2, c = 3) to verify.
1. What does the angle ratio a:b:c mean?
It represents the proportional relationship of the angles in the triangle, scaled to sum to 180°.
2. Can the ratios be negative?
No, angle ratios must be positive as angles in a triangle are positive values.
3. How are side length ratios calculated?
Side ratios are derived from the Law of Sines, proportional to the sines of the opposite angles, with the first side normalized to 1.
4. What if the angles don’t add to 180°?
The calculator ensures the sum is 180° by adjusting with the multiplier x; any deviation indicates invalid input.
5. Can I use this for any triangle?
Yes, this method works for any triangle as long as the ratio is valid and sums to a positive value.